今回のテーマは「デュードニー Part2」
2回前と同じテーマですが、今回はちょっと簡単になりました。
・問題
正方形と直角二等辺三角形の2つの図形を
出来るだけ少ない回数ではさみで切って組み合わせ
1つの大きな正方形を作りなさい
直角二等辺三角形を切ると、正方形に出来ますから
2つの図形の面積の和と同じ面積となる正方形の一辺は
2つの正方形のそれぞれの辺の1本抜き出して
直角三角形を作った時の対角線と等しくなります。
ですからその長さの線を出せるように切る必要があります。
汎用性のある正解(一般解)の図は下の通り
下の図では正方形の一辺と、直角三角形の斜辺の長さが
2:1となっている為に特殊な解が存在しますが、
下の正解図なら長さは関係なく
同じような手順を踏む事で必ず正方形が作れます。
(図のように正方形に直角三角形を付け
直角三角形が右に張り出した距離と同じだけ左上から点をずらし
そこから図のように2本の線を引けばOK)
今回は東大生チームが特殊解で解いてしまいまして、
一般解を導き出したマス北野が久しぶりに東大生チームに勝利。
マス北野の図形問題に対する直観力は凄いわ。
正解図
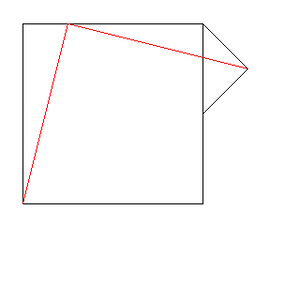
上のように切って……同色の部分に移せばOK。
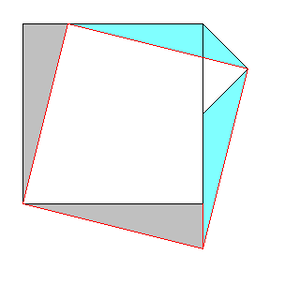

PR
