約1ヶ月ぶりのコマネチ大学。
今回のテーマは「スイッチングゲーム」
クロード・シャノンが作った問題、
情報系学科に行っていた自分にとっては馴染みのある問題です。
・問題
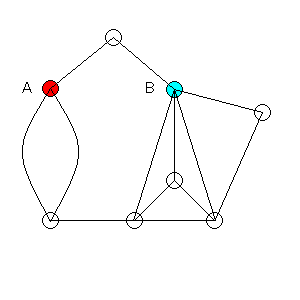
PLAYER 1(繋ぎ役):AからBまで線を繋げば勝ち
PLAYER 2(切り役):線を繋がせなければ勝ち
(補足)
下図にある13本の線をPLAYER 1とPLAYER 2が交互に自由に選択。
PLAYER 1が一度選んだ線は切る事が出来ません
PLAYER 2が一度選んだ線は繋ぐ事が出来ません。
繋ぐ線も切る線も、どこの線を選ぶのも自由です。
今回は力ずくで答えが出てしまう問題ですが、
証明するのは結構難しい問題。
竹内薫さんがグラフ理論で説明していましたが、
グラフ理論の原子にあたる部分の説明が少なすぎ。
あの原子に当たる図形は、どの地点をスタートとして始めても、
必ず全ての点に辿り着く事が出来る図形という事。
だからこそ、原子と同じ図形の部分は
考慮しなくても必ず辿り着けてしまう事となります。
この説明がテレビで放送されなかったのは残念。

PR
